Zalety i praktyczne aspekty niwelacji satelitarnej

NUMERUS

Technika satelitarna GNSS dobrze zadomowiła się i znalazła uznanie w produkcji geodezyjnej jako metoda pozyskiwania współrzędnych, natomiast nadal jest niedoceniona i rzadko stosowana przy zakładaniu osnów wysokościowych. Trudno ocenić dlaczego tak jest, można przypuszczać, że są to następujące powody:

obawa czy uzyskana dokładność niwelacji satelitarnej będzie zadawalająca
obawa czy taką metodę dopuszczają przepisy i zostanie zaakceptowana przez inspektora
brak szczegółowych wytycznych technicznych odnośnie technologii pomiaru i numerycznego opracowania niwelacji satelitarnej
brak wiedzy jak pomierzyć repery ścienne, gdzie pozornie wydaje się wykluczone zastosowanie niwelacji satelitarnej
brak oprogramowania do numerycznego opracowania niwelacji satelitarnej

Prawdopodobnie niemałe znaczenie ma też przyzwyczajenie z niwelacji klasycznej, gdzie wykonując pomiar między punktami A i B uzyskujemy natychmiast przewyższenie ΔH^AB. Natomiast wykonując pomiar odbiornikami GPS uzyskujemy wektor DX,DY,DZ, a nie poszukiwane przewyższenie. Nawet jeśli składowe przestrzenne pomierzonego wektora przeliczymy na przewyższenie Δh to będzie to przewyższenie elipsoidalne, a nie przewyższenie w obowiązującym systemie wysokości normalnych. Przewyższenie elipsoidalne Δh w żadnym przypadku nie może być bezpośrednio użyte do niwelacji, ponieważ wartość redukcji jest znaczna i w żadnym przypadku nie można ją zignorować.

W prawidłowym procesie numerycznym opracowania niwelacji satelitarnej powinien być wykorzystany model odstępów elipsoidy od quasigeoidy, ale bardzo ważne jest, w którym momencie procesu technologicznego i w jaki sposób z niego skorzystamy. Należy bowiem zdawać sobie sprawę, że każdy model odstępów obarczony jest pewnymi oczywistymi błędami własnymi i przy źle przeprowadzonych obliczeniach te błędy w całości skażą wynikowe rzędne punktów w państwowym układzie wysokościowym. Tak się stanie, jeśli pomierzoną sieć GNSS najpierw opracujemy jako sieć przestrzenną, a na końcu posłużymy się modelem geoidy do przelicznia wysokości elipsoidalnych na wysokości normalne. Natomiast dużo lepszą jakość wyniku uzyskamy, jeśli najpierw zredukujemy przewyższenia elipsoidalne Δh na przewyższenia normalne, a następnie wyrównamy tak uzyskane obserwacje jako sieć niwelacyjną. W tym przypadku błędy modelu odstępów elipsoidy od quasigeoidy będą miały o wiele mniejszy wpływ, ponieważ w pewnym sensie się znoszą - błąd różnicy odstępów geoidy pomiędzy dwoma punktami zawsze jest mniejszy niż bezwzględne błędy odstępów geoidy na każdym z tych punktów.

Obiektywnie rzecz biorąc niwelacja satelitarna może być bardzo atrakcyjną alternatywą dla niwelacji geometrycznej zwłaszcza tam, gdzie są znaczne długości pojedynczych odcinków albo trasa niwelacji przebiegałaby w niedostępnym bądź trudnym terenie, albo warunki pogodowe są niekorzystne.

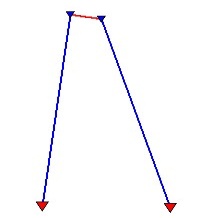
Zalety niwelacji satelitarnej możemy docenić chociażby w sytuacji, gdy realizowanemu obiektowi musimy zapewnić wyznaczenie wysokości w układzie państwowym ale niestety najbliższe repery osnowy wysokościowej znajdują się w odległości kilku lub kilkunastu kilometrów. Przykładem może być pomiar rzędnych kanalizacji w rejonie "nie uzbrojonym" w osnowę wysokościową. Niwelacja geometryczna oznacza wówczas sporo pracy, zwłaszcza jeśli teren jest trudny albo, co gorsza, po drodze jest np. rzeka. Natomiast za pomocą niwelacji satelitarnej możemy łatwo zrealizować chociażby konstrukcję pokazaną obok, dzięki czemu uzyskujemy na obiekcie dwa punkty pomiarowej osnowy wysokościowej, co rozwiązuje problem. Wystarczy satelitarny pomiar dwóch długich odcinków do reperów państwowych oraz geometryczny pomiar krótkiego odcinka pomiędzy nowymi punktami osnowy wysokościowej, który zamyka linię niwelacyjną. Tak zbudowany ciąg wyrównujemy w nawiązaniu do znanych reperów osnowy wysokościowej. Krótki odcinek też oczywiście może być pomierzony satelitarnie, ale jeśli pomierzony go niwelacją klasyczną to uzyskamy zarazem kontrolę całego zadania na wypadek, gdyby w zakresie niwelacji satelitarnej przydarzył się jakiś błąd.

Jakich dokładności możemy oczekiwać?

Na finalny błąd niwelacji satelitarnej składa się kilka elementów. Podstawowe to:
- błąd pomiaru GNSS,
- błąd modelu odstępów elipsoidy od quasigeoidy,
- ewentualny błąd przeniesienia wysokości z reperu na ekscentr GNSS (jeżeli reper jest ścienny).

Większość współczesnych odbiorników GPS oferuje dokładność pomiaru wysokości dla pomiaru statycznego nie gorszą niż 5 mm + 0.5 mm/km (patrz magazyn NAWI IV/2016 - zestawienie sprzętu GPS)

Błąd modelu odstępów elipsoidy od quasigeoidy PL-geoid-2011 jest szacowany na ok. 1 - 1.5 cm, ale jako błąd bezwzględny. W niwelacji satelitarnej posługujemy się różnicą odstępów, co powoduje oczywiste zmniejszenie interesującego nas błędu. Dlatego niwelacja satelitarna jest istotnie odporna na ewentualne niedoskonałości modelu geoidy. W tej sytuacji możemy przyjąć, że błąd z tytułu geoidy wynosi powiedzmy 4 mm, co i tak prawdopodobnie jest oszacowaniem zbyt pesymistycznym.

Błąd dobrze wykonanej niwelacji geometrycznej związanej z ewentualnym przeniesieniem wysokości z reperu na ekscentr GNSS nie powinien być większy niż 2 mm.

W efekcie uzyskujemy sumaryczny składnik stały błędu niwelacji satelitarnej

m² = (bł.odbiornika)² + (bł.geoidy)² + 2x(bł.ekscentru)² = 5² + 4² + 2x2² skąd m = 7.0 mm

a więc całkowity błąd niwelacji satelitarnej wynosi 7.0 mm + 0.5 mm/km przy jednokrotnym wyznaczeniu. Przy wyrównaniu z udziałem obserwacji nadliczbowych śmiało możemy oczekiwać wyniku dużo lepszego, a jego wyznacznikiem będą błędy średnie mh dla punktów uzyskane po wyrównaniu sieci.

Okazuje się, że przy długości odcinka rzędu kilku kilometrów niwelacja satelitarna w praktyce może być nawet "lepsza" niż wymagana dokładność niwelacji geometrycznej dla osnowy szczegółowej (4 mm/km).

Podstawa prawna i standardy techniczne

Nie ma przeciwskazań, żeby niwelację satelitarną stosować w przypadku pomiarowej osnowy wysokościowej. Rozporządzenie MR z dnia 18 sierpnia 2020 r w sprawie standardów technicznych wykonywania geodezyjnych pomiarów sytuacyjnych i wysokościowych wskazuje niwelację satelitarną jako jedną z metod zakładania pomiarowej osnowy wysokościowej. W §13 czytamy tu:

Pomiarową osnowę wysokościową realizuje się:
1) metodą niwelacji geometrycznej;
2) metodą niwelacji trygonometrycznej;
3) metodą niwelacji satelitarnej z wykorzystaniem techniki statycznej GNSS;
4) techniką statyczną GNSS z wykorzystaniem obliczeń postprocessingu;
5) techniką kinematyczną GNSS.

Istotny jest również §14 i jego następujące punkty:

1. Dane obserwacyjne pozyskane przy wykonywaniu pomiarów, o których mowa w §13 pkt. 1-3 , wyrównuje się metodą najmniejszych kwadratów w układzie sieci jednorzędowej w dowiązaniu do co najmniej dwóch punktów wysokościowej osnowy geodezyjnej przy założeniu bezbłędności punktów nawiązania.
2. Podczas zakładania pomiarowej osnowy wysokościowej z wykorzystaniem techniki GNSS w przypadku braku możliwości wykonania pomiaru bezposrednio na punkcie dopuszcza się przeniesienie wysokości na reper roboczy za pomocą metod o któreych mowa w §13 pkt. 1 lub 2.
4. Wyznaczenie wysokości z wykorzystaniem technik, o których mowa w §13 pkt. 4 i 5, realizowane jest przez wpasowanie matematyczne w oparciu o punkty łaczne lub za pomocą przeliczenia wysokości elipsoidalnej do wysokości w państwowym układzie wysokościowym z uwzględnieniem obowiązujacego modelu quasigeoidy.
5. Miarą dokładności pomierzonej osnowy wysokościowej są błędy średnie wysokości jej punktów po wyrównaniu, a w przypadku zakładania osnowy pomiarowej technikami kinematycznymi GNSS - dokładność wykorzystanego serwisu pozycjonowania.

Od 2021 roku przepisy pozwalają na stosowanie niwelacji satelitarnej również w przypadku szczegółowej osnowy wysokościowej. Można traktować to jako wyraz urzędowego zaufania, że metoda kwalifikuje się i podoła wymaganiom. Zezwala na to rozporzadzenie MRPiT z dnia 6 lipca 2021 r. w sprawie osnów geodezyjnych, grawimetrycznych i magnetycznych. W Załączniku nr 1 tegoż rozporządzenia, w rozdziale 7, w paragrafie 1 napisano:

1. Szczegółową osnowę geodezyjną wysokościową tworzą punkty, których wysokości wyznaczono metodą:
1) niwelacji geometrycznej;
2) niwelacji satelitarnej.

Inne paragrafy tego rozporządzenia zwracają tylko uwagę na konieczność zadbania o warunki pomiaru GNSS, obowiązek nawiazania sieci na repery osnowy wyższego rzędu oraz konieczność przestrzegania odpowiedniej procedury obliczeń, co jest rzeczą oczywistą.

Na podstawie dotychczasowych ustaleń i cytowanych rozporządzeń możemy sformułować najważniejsze wskazówki praktyczne:

Ze względów dokładnościowych niwelację satelitarną najlepiej wykonywać za pomocą metody statycznej GNSS ale w przypadku osnowy pomiarowej dopuszcza się też technikę kinematyczną. Miarą jakości wykonanej niwelacji będą błędy średnie wysokości punktów po wyrównaniu, co decyduje czy efekt końcowy spełnia wymagane kryteria dokładnościowe.
Niwelację tego rodzaju można realizować poprzez pomiar wektorów pomiędzy sąsiednimi punktami (reperami). Z tak pomierzonych wektorów, po przekształceniu w przewyższenia normalne, można budować ciągi niwelacyjne podlegające wyrównaniu w nawiązaniu reperów osnowy wyższego rzędu. Pozwala to pojęciowo traktować niwelację satelitarną analogicznie do niwelacji klasycznej, gdzie właśnie z pomierzonych odcinków budowane są linie niwelacyjne, a linie lub złożone z nich sieci zostają wyrównane ściśle w nawiązaniu do reperów wyższego rzędu. Różnica polega tylko w rodzaju użytych narzędzi pomiarowych.
Na większych obiektach, mierzonych zwykle z użyciem większej liczby odbiorników, śmiało można stosować sieciową metodę pomiaru. Uzyskane wektory "poprzeczne" są również do wykorzystania i przyczynią się do wzmocnienia konstrukcji sieci.
Przed wyrównaniem obserwacje satelitarne bezwzględnie podlegają konwersji na przewyższenia normalne z zastosowaniem obowiązującego modelu quasigeoidy.
Odcinki niwelacji satelitarnej mogą tworzyć samodzielną grupę obserwacji podlegających wyrównaniu albo mogą wchodzić w skład sieci hybrydowej złożonej z niwelacji satelitarnej i niwelacji geometrycznej podlegających łącznemu wyrównaniu. Taka możliwość posiada bardzo przydatną zaletę, ponieważ dla konkretnego obiektu pozwala na dobranie najbardziej ekonomicznej metody pomiaru, na przykład metoda satelitarna dla długich odcinków, a metoda geometryczna dla krótkich.

Potrzebne jest oprogramowanie

Zobacz filmy na YouTube
wyrównanie niwelacji satelitarnej lub hybrydowej - przykład 1
wyrównanie niwelacji satelitarnej lub hybrydowej - przykład 2j
niwelacja satelitarna metodą RTN - metoda pomiaru i wyrównanie>

Niwelacja satelitarna wymaga użycia specjalistycznego oprogramowania, które umożliwi konwersję wektorów na przewyższenia normalne a następnie wyrównanie ciągu lub bardziej złożonej sieci niwelacyjnej. Program UltraNet jest właśnie narzędziem dobrze spełniającym wszystkie wymagania w tym zakresie.
Na całość opracowania numerycznego składają się dwa etapy:

Etap 1 - obliczenie współrzędnych punktów koniecznych w procesie redukcji obserwacji oraz przekształcenie wektorów w przewyższenia normalne. W przypadku większej sieci możemy na tym etapie uzyskać również weryfikację jakości wektorów i wyeliminować obserwacje wadliwe, ponieważ cały proces odbywa się na zasadzie wyrównania przestrzennego.
Etap 2 - wyrównanie sieci niwelacyjnej złożonej z odcinków niwelacji satelitarnej albo sieci hybrydowej zawierającej przewyższenia satelitarne i przewyższenia klasyczne.

Uwagi praktyczne

Ze względów dokładnościowych najlepszą metodą realizacji niwelacji satelitarnej jest wykorzystanie techniki statycznej GNSS. Niestety nie dla wszystkich taka metoda może być dostępna, ponieważ wymaga to posiadania co najmniej dwóch odbiorników GPS oraz aplikacji do wykonywania postprocessingu.
W pewnych prostszych zastosowaniach i mniejszych wymaganiach dokładnościowych możliwe jest wykorzystanie metody kinematycznej RTN, przy zachowaniu odpowiedniej procedury pomiaru. Niewątpliwą zaletą tej metody jest możliwość pomiaru tylko jednym odbiornikiem przemieszczanym z punktu na punkt.

W przypadku metody statycznej ilość istotnych wektorów uzyskiwanych w jednej sesji zależy od liczby odbiorników biorących udział w pomiarze. Jeśli wektorów jest kilka lub kilkanaście to do niwelacji satelitarnej możemy wybrać tylko te wektory, które łączą sąsiednie punkty i tworzą układ analogiczny do ciągu klasycznej niwelacji. Dodanie innych, "poprzecznych" wektorów powstających z dodatkowych relacji pomiędzy odbiornikami nie jest błędem. Przyczynia się to do wzmocnienia konstrukcji sieci ale zazwyczaj są to wektory dłuższe, a więc mniej dokładne.

Operacja przekształcenia pomierzonych wektorów w odpowiadajace im przewyższenia niwelacyjne wymaga współrzędnych końcowych punktów tych wektorów. Program UltraNet potrafi obliczyć takie współrzędne na podstawie jednego lub minimalnego zestawu punktów "startowych", analogicznie jak to się dzieje przy wyrównaniu sieci 3D.
W przypadku metody statycznej istnieją dwa sposoby umożliwiające spełnienie takich warunków "startowych".

Zadanie współrzędnych i wysokości (lub współrzędnych XYZ) dla co najmniej jednego punktu oraz dodanie do obserwacji wektorów umożliwiających przeniesienie tych współrzędnych na pozostałe punkty obiektu. Punkt ten de facto nie biorze potem udziału w niwelacji, pełni jedynie funkcję pomocniczą w pierwszym etapie obliczeń.
Takim punktem może być punkt osnowy geodezyjnej, stacja referencyjna ASG-EUPOS lub tzw. punkt wirtualny VRS wygenerowany za pomocą systemu ASG-EUPOS.
Zadanie współrzędnych co najmniej jednego punktu biorącego udział w niwelacji satelitarnej. Wystarczą tu jego współrzędne przybliżone z dokładnością kilku metrów, a więc mogą to być współrzędne pochodzących z rozwiązania typu SPP (Single Point Positioning) uzyskanego w trakcie postprocessingu.

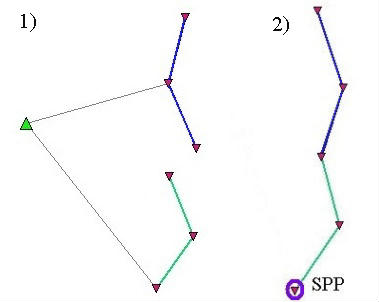
Na rysunkach obok widzimy szkice przykładowych obiektów, dla których wykonano po dwie sesje pomiarowe (niebieska i zielona), a w każdej sesji pomierzono dwa wektory służące potem do niwelacji satelitarnej.
W przykładzie z lewej strony do obliczenia współrzędnych służy punkt osnowy poziomej, więc dane zawierają również wektory (zasygnalizowano minimalny zestaw) pozwalające przenieść te współrzędne na pozostałe punkty obiektu.
W przykładzie z prawej strony podano współrzędne typu SPP dla jednego punktu sieci. Wszystkie punkty są powiazane konstrukcyjne, więc ten jeden punkt wystarczy, żeby program obliczył sobie współrzędne pozostałych punktów sieci.

W przypadku metody RTN musimy zastosować nieco odmienną procedurę pomiaru i pozyskania danych potrzebnych do obliczeń.

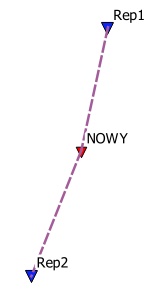
Przykładowo chcemy wyznaczyć wysokość nowego punktu wysokościowego w nawiązaniu do dwóch znanych reperów, tak żeby dochowany był warunek kontroli i pomiarów nadliczbowych.

Gdyby to była metoda statyczna to pomierzylibyśmy po prostu wektory pokazane na rysunku. Natomiast metodą RTN nie możemy zrealizować takich wektorów, ponieważ posługujemy się tylko jednym odbiornikiem, a więc nie ma warunków do pomiaru synchronicznego. Nie możemy też posłużyć się postprocessingiem, który w metodzie statycznej dostarcza nam skladowych dX, dY, dZ dla każdego wektora.

Zastosujemy więc tu inną metodę postępowania.

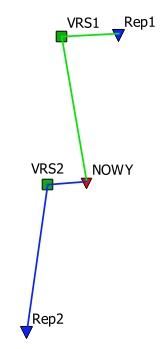
Wykonamy inicjalizację odbiornika na reperze Rep1, odbiornik wygeneruje wirtualną stację bazową, którą oznaczono tu umownie VRS1. Wykonujemy pomiar na tym reperze a następnie przemieszczamy się na punkt wyznaczany NOWY ale ważne jest, żeby nie nastąpiło wygenerowania nowej, wirtualnej stacji bazowej. Uzyskujemy w ten sposób obserwacje sesji "zielonej".
Następnie wykonujemy nową incjalizację, czyli zostaje wygenerowana wirtualna stacja bazowa VRS2. Mierzymy ponownie punkt NOWY a następnie reper Rep2. Podobnie jak poprzednio oba punkty muszą być pomierzone przy tej samej stacji bazowej. Uzyskujemy w ten sposób obserwacje dla sesji "niebieskiej".

Składowe dX, dY, dZ poszczególnych wektorów pobieramy z raportu pomiaru RTN. Z tego samego raportu pobieramy współrzędne wirtualnych stacji bazowych potrzebne w pierwszej fazie obliczeń do konwersji wektorów na przewyższenia normalne. Dobry raport pomiaru RTN powinien zawierać wszystkie te dane, ewentualnie możemy je pozyskać za pomocą programu UltraNet wprost z pliku odbiornikowego rw5.

Jeżeli pomierzone wektory zamienimy na przewyższenia normalne to w efekcie uzyskamy linię niwelacyjną złożoną z czterech wektorów oraz podwójne wyznaczenie nowego punktu w nawiązaniu do dwóch niezależnych reperów. Po wyrównaniu takiej "sieci" niwelacyjnej otrzymamy wysokość nowego punktu.

W tej metodzie pomiaru nie ma znaczenia błąd wyznaczenia wirtualnej stacji bazowej. Wykorzystujemy tu tylko wektory pomiędzy stacją bazową i punktami mierzonymi, które są relatywnie krótkie, a więc dokładniejsze niż sama stacja bazowa.
Punkty VRS1 i VRS2 wystąpią również w naszych obliczeniach ale w zupełnie innej roli - nie jako punkty "zadane", wyznaczone przez odbiornik lecz jako matematyczne punkty wyznaczane pełniące jedynie rolę pomocniczych punktów pośrednich.
Punkt wyznaczany nie otrzymuje wysokości z nawiązania na odległe stacje referencyjne ASG-EUPOS lecz z nawiązania na repery zlokalizowane na obiekcie.
Po wykonaniu wyrównania otrzymujemy obiektywną ocenę dokładności wyznaczanych punktów w postaci błędu średniego mh co decyduje czy dokładność naszego pomiaru spelnia kryteria dokladnościowe wymagane dla tych punktów.

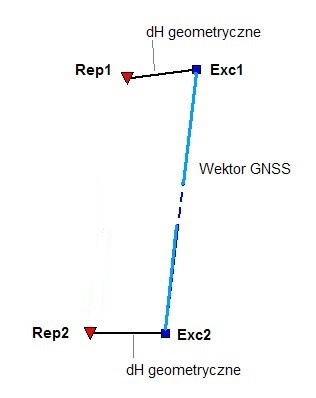
Pewną niedogodnością niwelacji satelitarnej jest brak możliwości bezpośredniego pomiaru reperów ściennych. Rozwiązanie tego problemu sugeruje chociażby wyżej wspomniane rozporządznie w §14 pkt.2, czyli pomiar GNSS realizowany na tymczasowym ekscentrze, którego lokalizację dobrano z uwzględnieniem wymagań techniki GPS, założonym w pobliżu reperu. Przeniesienie wysokości z ekscentru na reper główny zazwyczaj jest możliwe do wykonania za pomocą jednostanowiskowej niwelacji geometrycznej.

Na rysunku obok przedstawiono szkic poglądowy dla odcinka, gdzie akurat oba końce to repery ścienne. W pobliżu reperów założono punkty ekscentryczne, pomiędzy którymi można już pomierzyć wektor metodą GNSS. Za pomocą niwelacji geometrycznej należy pomierzyć również przewyższenia pomiędzy każdym reperem oraz jego ekscentrem. Oba rodzaje przewyższeń - satelitarne i te wynikające z przeniesienia wysokości na reper stanowią dane wejsciowe do finalnego, hybrydowego wyrównania niwelacji, co załatwia problem reperów ściennych.

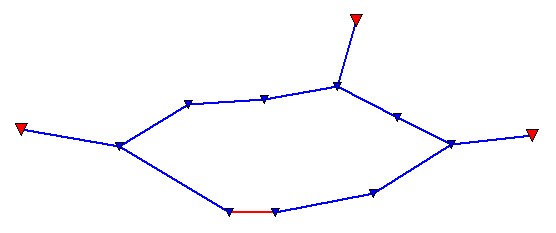
Podobnie jak w przypadku niwelacji klasycznej, z odcinków niwelacji satelitarnej można bydować linie niwelacyjne oraz sieci wielowęzłowe. Zawsze finalnym etapem powinno być wyrównanie metodą najmniejszych kwadratów w nawiązaniu do reperów wyższego rzędu.

Wyrównaniu powinien podlegać zarówno pojedynczy ciąg, każda bogatsza konstrukcja wielowęzłowa, jak i złożone sieci niwelacyjne.

W łącznym wyrównaniu mogą uczestniczyć odcinki niwelacyjne pozyskane ewentualnie różnymi technologiami pomiaru - za pomocą niwelacji satelitarnej oraz za pomocą klasycznej niwelacji geometrycznej, ale należy zadbać o poprawne wzajemne zwagowanie obu grup obserwacji.